はんだ理論10
相図(状態図)
はんだをはじめとする合金など、多成分でできた物質の組成や温度による状態を 表したものが相図、または状態図と言われる物です。 合金の状態は、組み合わせる金属の種類により変わります。合金の状態を考える ために下に 2 つの金属を合金化した相図の例を示します。
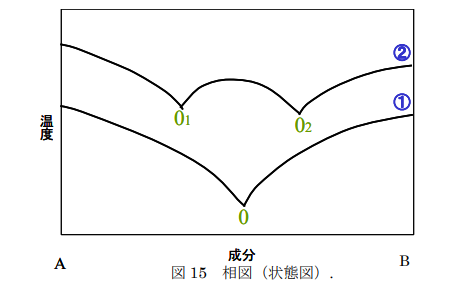
A,と B はそれぞれ成分の違う金属です。横軸の左端は A 成分 100%(B 成分は 0%)、左端は B 成分 100%(A 成分は 0%)を表しています。横軸のちょうど真ん 中が A 成分 50%、B 成分 50%のところになります。
縦軸は温度を表しています。上に行くほど温度が高いと考えてください。また、 ①と②の曲線のデータは融点を表しています。
(データの曲線の上では液体、線の下 では固体ということです。)
曲線①で示したデータは、A 成分と B 成分で化合物が生成しない組み合わせの場 合の曲線データです。 A と B の 2 種類の金属を混ぜ合わせると A、B が 100%の場合より融点は下がり ます。
(A と B の混合比によって融点は異なります。)
例えば A が 100%から B を少 し加えていくと(図 15 では成分の軸が左端から少しずつ右に向かう)と少しずつ 融点が下がっていきます。そしてある割合で融点が一番低い状態になります。
図 15 の「0」の地点です。そこから B の成分が増えていくに従い、融点は上がってい き、B が 100%の場所、すなわちグラフの右端では B が 100%の場合の融点になり ます。
この①のグラフで「0」の点 = 融点が一番低い点は「共晶点」といいます。ギブ スの相律で考えると、共晶点以外の①の曲線上では相の数 P は「固相」と「液相」 の 2、成分の数 C は 2 になるので
(8)式より

となり自由度は 2 になります。しかし「共晶点」では A 成分と B 成分による合金の 液相」と「A 成分の固相」と「B 成分の固相」の 3 つの相が共存する状態です。す なわち(8)式では P =3、C=1 になり
(8)式は、

となり、F = 0 になります。 「共結点」を持つためには各成分の混合比は決まっています。(図の「0」点の混合 比)
その混合比で混ざり合った物質は固体から液体に変わる場合、A と B が一定の 割合で溶解していきます。逆に液体から固体に変わる場合も、A と B が一定の割合 で晶出(固体になる)します。

次に曲線②で示したデータは、A と B の両成分の間に化合物が精製される場合の 曲線データです。
「01」の点は A と B の化合物と A の共晶点、「02」の点は A と B の化合物と B の共晶点になります。
「01」と「02」の間の曲線部分は A,B 化合物の融点を表して います。 共晶はんだは Sn と Pb が化合物を作らないので、共晶点を持ちます。
(共晶はん だと言われるのですから言葉通りですね。) 次回は相図を元に、共晶の意味についてもう少し詳しく考えて行きましょう。